Vor einiger Zeit gab es in einem anderen Board eine Diskusion über die sogenannten "Modeler", was für mich den Grund geliefert hat, mir einmal ein paar grundsätzliche Gedanken zu dem Thema zu machen:
Modeler vs. Analog
Bis vor kurzem wurden Übertragungssysteme ausschließlich als analoge Lösung realisiert. Als Grundbestandteile wurden Spulen, Kondensatoren, Widerstände, Dioden und Transistoren verwendet. Das man die damit realisierten Funktionen auch in zeit- und wertdiskreter Form realisieren konnte, hatte lange Zeit nur theoretische Bedeutung, da Speicher und schnelle Signalprozessoren (DSP) sehr teuer und/oder nicht verfügbar waren.
Bei diesem Verfahren werden die analogen Komponenten durch digitale Verzögerungsglieder, Addierer und Mutiplizierer ersetzt. Dabei lassen sich Verzögerugsglieder durch Speicher realisieren und die Rechenoperationen sind eine typische Domäne eines Mikroprzessors.
Man benötigt also Speicher, DSP und die beiden Wandler (Analog zu Digital und Digital zu Analog) und natürlich ein Programm, den sogenannten Algorithmus.
1. Eigenschaften eines Übertragungssystems (Verstärker)
Ein Übertragungssystem ist in der Lage folgende Veränderungen an einem am Eingang angelegten Signal vorzunehmen:
1.1 Lineare Verstärkung
Eine angelegte Signalgröße wird um einen konstanten Faktor vergrößert (Verstärkung) oder verringert (Dämpfung). Es ist dabei unerheblich, ob es sich Gleichspannung oder Wechselspannung handelt. Alle Frequenzen (auch f=0Hz) werden um diesen Faktor verändert.
Beispiel:
Ua= a*Ue (a<1: Dämpfung, a>1: Verstärkung)
Besteht das Eingangsignal also aus einem Frequenzgemisch, wird dieses Gemisch insgesamt verändert. Eine Änderung der Signalinformation wird dabei nicht erzeugt!
Diese Veränderung wird in der Praxis durch einen Verstärker oder einen Spannungsteiler realisiert, die für unser Verständnis jedoch als ideal aufzufassen sind!
1.2 Lineare Verzerrung
Regt man ein System mit einem Dirac-Puls an, so entspricht die Systemantwort im Frequenzbereich exakt seiner Übertragungsfunktion. Der in der Regelungstechnik übliche Weg über die Sprungantwort basiert auf praktischen Überlegungen, führt letztendlich aber zum gleichen Ziel.
Bei der linearen Verzerrung handelt es sich wiederum um eine Verstärkung. Allerdings ist diese frequenzabhängig. Die Übertragungsfunktion eines elektromagnetischen Tonabehmers ist ein gutes Beispiel dafür:
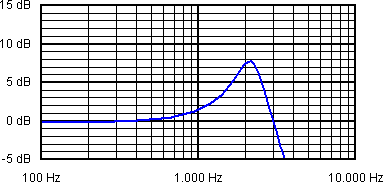
Hier ist zu erkennen, daß Frequenzen unter 1 kHz nicht verstärkt werden (~0dB), der Bereich zwischen 1 und 3 kHz verstärkt wird und ab 3kHz eine Dämpfung eintritt.
Im Gegensatz zur linearen Verstärkung wird hier also das Verhältnis der Amplituden der einzelnen Frequenzen verändert. Im akustischen Verständnis könnte man sagen, daß eine "Klangumformung" oder "Verfärbung" stattfindet.
Mathematisch muß dieses Verhalten durch komplexe Gleichung beschrieben werden. Eingebürgert hat sich die Darstellung im Frequenzbereich, die durch die sogenannte Fouriertransformation mit dem Zeitbereich verbunden ist.
Ua(j*w)=G(j*w)*Ue(j*w) (darin ist G(j*w) die Übertragungsfunktion)
Lineare Verzerrungen werden in der Praxis durch sogenannte Filter realisiert. Ein Equalizer ist ein gutes Beispiel für einen solchen linearen Verzerrer.
1.3 Nichtlineare Verzerrung
Wir betreten jetzt einen Bereich, der für die reine Übertragungstechnik eigentlich unerwünscht ist. Für Modulation und Demodulation ist er jedoch notwendig und auch die Gitarristen mögen gerne nichtlineare Verzerrungen.
Diese Art von Verzerrung entsteht durch die Aussteuerung einer nichtlinearen Kennlinie, wie sie bei Röhren und Halbleitern Gang und Gebe ist.
Man kann vereinfacht sagen, daß die Verstärkung des Systems eine von der Eingangsspannung abhängige Größe ist.
Ua=a(Ue)*Ue
Das bedeutet, daß unabhängig von der Frequenz die Ausgangsspannung nur von der Eingangsamplitude beeinflußt wird.
In der Praxis werden die nichtlinearen Kennlinien gerne durch ein Knickkennlinie oder eine quadratische Funktion angenähert.
Ua=a*Ue^2
Das sich dadurch die Signalform am Ausgang verändert, ist leicht einsehbar. Bei einer Sinusaussteuerung kann die Signalform am Ausgang von einem ein- oder beidseitig abgeplatteten Sinus bis zu einem Rechteck variieren.
Auch wenn man es optisch auf einem Oszilloskop nicht mehr sehen kann, ist das Ergebnis einer solchen Verzerrung "hörbar". Unterwirft man das Ausgangssignal einer Fourieranalyse, so stellt man fest, daß zusätzliche Frequenzen im Spektrum auftauche, die im Eingangssignal nicht enthalten waren. Je nachdem, ob es sich um Vielfache der Eingangsfrequenz handelt oder nicht, empfinden wir das Resultat als "klingend" oder als Geräusch.
Analog zur linearen Verzerrung muß man bei der nichtlinearen Verzerrung von einer "Klangerweiterung" sprechen.
Da zusätzliche Frequenzen entstehen, ändert sich auch die Information des Signales. Wir hören jetzt ja ein anderes Klangereignis!
2. Der Verstärker
2.1 Die analoge Welt
Bevor man sich mit der digitalen Nachbildung eines Verstärkers befaßt, sollte man die analoge Realisierung genau analysieren. Betrachten wir einmal die bekannte Verstärkerschaltung. Dabei spielt es erst einmal keine Rolle, ob ein Transistor oder eine Röhre verwendet wird.
2.2 Verstärker goes digital...
Möchte man das eben beschriebene Verhalten digital nachbilden, so sind mehrere Dinge notwendig:
2.3 Der Teufel steckt im Detail
Da wir jetzt wissen, welche digitalen System wir benötigen, kann man das ganze ja mal schnell zusammenprogrammieren. Aber so einfach ist das leider nicht, denn es kann von entscheidender Bedeutung sein, an welcher Stelle der Kette die Nachbildung der Verzerrung erfolgt. Wer schon einmal mit einen Equalizer vor und nach einem Verzerrer experimentiert hat weiß, daß bezüglich der Wirksamkeit und des Effektes große Unterschiede bestehen.
Es gibt viele kleine Dinge, die das Resultat nicht zu 100 Prozent vergleichbar machen können:
In der Praxis wird man sicherlich eine Kombination beider Methoden wählen.
2.4 Das Modell eines Instrumentenverstärkers
Das, was für eine Verstärkerstufe gilt, muß natürlich auch für einen gesamten Verstärker gelten. Es macht jedoch keinen Sinn, das gesamte Gerät als Box mit einem Eingang und Ausgang zu verstehen und die Meßergebnisse in eine digitale Lösung umzusetzen. Dabei bleiben zu viele Details auf der Strecke. Der bessere Weg ist dieser:
3. Ein Modeler klingt schlecht!
Das muß allerdings nicht so sein. Der zu treibende Entwicklungsaufwand ist jedoch nicht unerheblich und kann in der Regel nur von Elektroingenieuren geleistet werden. Dementsprechend entstehen hier hohe Kosten. Damit dürfte auch klar geworden sein, warum die billigen Modeler tatsächlich schlecht klingen. Man hat aus Zeit- und Kostengründen einfach nicht sorgfältig genug gearbeitet und quasi die Hälfte vergessen!
Zusammenfassung
Mit Hilfe der Methoden der digitalen Signalverarbeitung läßt sich ein analoger Verstärker vollständig nachbilden (Gleiches gilt übrigens auch für die Modellierung von Effekten).
Die Qualität und damit das klangliche Ergebnis steht und fällt mit der Qualität der verwendeten analogen Modelle des zu modellierenden Verstärkers.
Ulf
Modeler vs. Analog
Bis vor kurzem wurden Übertragungssysteme ausschließlich als analoge Lösung realisiert. Als Grundbestandteile wurden Spulen, Kondensatoren, Widerstände, Dioden und Transistoren verwendet. Das man die damit realisierten Funktionen auch in zeit- und wertdiskreter Form realisieren konnte, hatte lange Zeit nur theoretische Bedeutung, da Speicher und schnelle Signalprozessoren (DSP) sehr teuer und/oder nicht verfügbar waren.
Bei diesem Verfahren werden die analogen Komponenten durch digitale Verzögerungsglieder, Addierer und Mutiplizierer ersetzt. Dabei lassen sich Verzögerugsglieder durch Speicher realisieren und die Rechenoperationen sind eine typische Domäne eines Mikroprzessors.
Man benötigt also Speicher, DSP und die beiden Wandler (Analog zu Digital und Digital zu Analog) und natürlich ein Programm, den sogenannten Algorithmus.
1. Eigenschaften eines Übertragungssystems (Verstärker)
Ein Übertragungssystem ist in der Lage folgende Veränderungen an einem am Eingang angelegten Signal vorzunehmen:
- Lineare Verstärkung,
- Lineare Verzerrung,
- Nichtlineare Verzerrung
1.1 Lineare Verstärkung
Eine angelegte Signalgröße wird um einen konstanten Faktor vergrößert (Verstärkung) oder verringert (Dämpfung). Es ist dabei unerheblich, ob es sich Gleichspannung oder Wechselspannung handelt. Alle Frequenzen (auch f=0Hz) werden um diesen Faktor verändert.
Beispiel:
Ua= a*Ue (a<1: Dämpfung, a>1: Verstärkung)
Besteht das Eingangsignal also aus einem Frequenzgemisch, wird dieses Gemisch insgesamt verändert. Eine Änderung der Signalinformation wird dabei nicht erzeugt!
Diese Veränderung wird in der Praxis durch einen Verstärker oder einen Spannungsteiler realisiert, die für unser Verständnis jedoch als ideal aufzufassen sind!
1.2 Lineare Verzerrung
Regt man ein System mit einem Dirac-Puls an, so entspricht die Systemantwort im Frequenzbereich exakt seiner Übertragungsfunktion. Der in der Regelungstechnik übliche Weg über die Sprungantwort basiert auf praktischen Überlegungen, führt letztendlich aber zum gleichen Ziel.
Bei der linearen Verzerrung handelt es sich wiederum um eine Verstärkung. Allerdings ist diese frequenzabhängig. Die Übertragungsfunktion eines elektromagnetischen Tonabehmers ist ein gutes Beispiel dafür:

Hier ist zu erkennen, daß Frequenzen unter 1 kHz nicht verstärkt werden (~0dB), der Bereich zwischen 1 und 3 kHz verstärkt wird und ab 3kHz eine Dämpfung eintritt.
Im Gegensatz zur linearen Verstärkung wird hier also das Verhältnis der Amplituden der einzelnen Frequenzen verändert. Im akustischen Verständnis könnte man sagen, daß eine "Klangumformung" oder "Verfärbung" stattfindet.
Mathematisch muß dieses Verhalten durch komplexe Gleichung beschrieben werden. Eingebürgert hat sich die Darstellung im Frequenzbereich, die durch die sogenannte Fouriertransformation mit dem Zeitbereich verbunden ist.
Ua(j*w)=G(j*w)*Ue(j*w) (darin ist G(j*w) die Übertragungsfunktion)
Lineare Verzerrungen werden in der Praxis durch sogenannte Filter realisiert. Ein Equalizer ist ein gutes Beispiel für einen solchen linearen Verzerrer.
1.3 Nichtlineare Verzerrung
Wir betreten jetzt einen Bereich, der für die reine Übertragungstechnik eigentlich unerwünscht ist. Für Modulation und Demodulation ist er jedoch notwendig und auch die Gitarristen mögen gerne nichtlineare Verzerrungen.
Diese Art von Verzerrung entsteht durch die Aussteuerung einer nichtlinearen Kennlinie, wie sie bei Röhren und Halbleitern Gang und Gebe ist.
Man kann vereinfacht sagen, daß die Verstärkung des Systems eine von der Eingangsspannung abhängige Größe ist.
Ua=a(Ue)*Ue
Das bedeutet, daß unabhängig von der Frequenz die Ausgangsspannung nur von der Eingangsamplitude beeinflußt wird.
In der Praxis werden die nichtlinearen Kennlinien gerne durch ein Knickkennlinie oder eine quadratische Funktion angenähert.
Ua=a*Ue^2
Das sich dadurch die Signalform am Ausgang verändert, ist leicht einsehbar. Bei einer Sinusaussteuerung kann die Signalform am Ausgang von einem ein- oder beidseitig abgeplatteten Sinus bis zu einem Rechteck variieren.
Auch wenn man es optisch auf einem Oszilloskop nicht mehr sehen kann, ist das Ergebnis einer solchen Verzerrung "hörbar". Unterwirft man das Ausgangssignal einer Fourieranalyse, so stellt man fest, daß zusätzliche Frequenzen im Spektrum auftauche, die im Eingangssignal nicht enthalten waren. Je nachdem, ob es sich um Vielfache der Eingangsfrequenz handelt oder nicht, empfinden wir das Resultat als "klingend" oder als Geräusch.
Analog zur linearen Verzerrung muß man bei der nichtlinearen Verzerrung von einer "Klangerweiterung" sprechen.
Da zusätzliche Frequenzen entstehen, ändert sich auch die Information des Signales. Wir hören jetzt ja ein anderes Klangereignis!
2. Der Verstärker
2.1 Die analoge Welt
Bevor man sich mit der digitalen Nachbildung eines Verstärkers befaßt, sollte man die analoge Realisierung genau analysieren. Betrachten wir einmal die bekannte Verstärkerschaltung. Dabei spielt es erst einmal keine Rolle, ob ein Transistor oder eine Röhre verwendet wird.
- Durch die Beschaltung mit Widerständen macht die Schaltung eine lineare Verstärkung. Das ist genau das, was sie ja auch tun soll. Aber
- durch die Kapazitäten (Trennkondensatoren zur Arbeitspunktabsicherung,...) und die Widerstände entsteht jedoch auch ein frequenzabhängiges Verhalten. Es ergeben sich dadurch in erster Linie drei Hochpässe.
Da das Verstärkerelement (Transistor, Röhre) auch über parasitäre Kapazitäten verfügt, entstehen noch weitere Filter, die in aller Regel ein Tiefpaßverhalten zur Folge haben. Über alles entsteht dann meist ein sogenannter Bandpaß. Wir haben also jede Menge linearer Verzerrer im Spiel.
- Die Kennlinien des aktiven Elementes sind nur innerhalb eines gewissen Aussteuerbereiches annähernd linear. Durch gezielte Gegenkopplung wird versucht, diesen Bereich zu vergrößern.
2.2 Verstärker goes digital...
Möchte man das eben beschriebene Verhalten digital nachbilden, so sind mehrere Dinge notwendig:
- Nachbildung der linearen Verstärkung
Das ist relativ einfach. Das digitalisierte Signal wird einfach mit einer konstanten Größe multipliziert.
- Nachbildung der linearen Verzerrung
Hier müssen mehrere analoge Filter digital nachgebildet werden. Dazu ist es unbedingt notwendig, die entsprechenden Übertragungsfunktionen zu kennen. Sie werden dann mathematisch abgetastet. Dabei kommt dann die sogenannte Z-Transformation zum Einsatz.
G(j*w) -> H(z)
Am Ende der Prozedur steht dann ein Algorithmus, der aus Verzögerungen, Addierern und Multiplizieren besteht. Die Koeffizienten für die Multiplizierer ergeben sich aus der Übertragungsfunktion H(z).
Die Realisierung solcher Filter mit Hilfe eines DSP stellt heute kein großes Problem mehr dar.
- Nachbildung der nichtlinearen Verzerrung
Hier wird es schon etwas schwieriger. Grundsätzlich muß man die nichtlineare Kennlinie digital nachbilden. Da sich eine geschlossene mathematische Beschreibung in der Regel als schwierig und daher ungenau erweist, wird das ganze häufig durch eine Tabelle gelöst.
In ihr wird jedem möglichen Wert der Eingangsspannung der entsprechende Wert der Ausgangsspannung zugeordnet. Da bei einem digitalen Signal die Wertemenge der Amplitude begrenzt ist, kann man den Eingangswert hervorragen als Index benutzen, um so aus einem mit Werten belegten Array den notwendigen Ausgangswert auszulesen.
2.3 Der Teufel steckt im Detail
Da wir jetzt wissen, welche digitalen System wir benötigen, kann man das ganze ja mal schnell zusammenprogrammieren. Aber so einfach ist das leider nicht, denn es kann von entscheidender Bedeutung sein, an welcher Stelle der Kette die Nachbildung der Verzerrung erfolgt. Wer schon einmal mit einen Equalizer vor und nach einem Verzerrer experimentiert hat weiß, daß bezüglich der Wirksamkeit und des Effektes große Unterschiede bestehen.
Es gibt viele kleine Dinge, die das Resultat nicht zu 100 Prozent vergleichbar machen können:
- Die Reihenfolge von Verstärker, Filter
 und Verzerrer
und Verzerrer
- Die Auflösung der Lockup-Table für den Verzerrer
- Die Realisierung der Filter
- Übertragungsfehler durch ADC und DAC.
In der Praxis wird man sicherlich eine Kombination beider Methoden wählen.
2.4 Das Modell eines Instrumentenverstärkers
Das, was für eine Verstärkerstufe gilt, muß natürlich auch für einen gesamten Verstärker gelten. Es macht jedoch keinen Sinn, das gesamte Gerät als Box mit einem Eingang und Ausgang zu verstehen und die Meßergebnisse in eine digitale Lösung umzusetzen. Dabei bleiben zu viele Details auf der Strecke. Der bessere Weg ist dieser:
- Zerlegung des analogen Verstärkers in einzelne Stufen.
- Analoge Modellierung der einzelnen Stufen.
- Digitalisierung der analogen Modelle (Algorithmen).
- Verkettung der einzelnen Algorithmen zu einer Gesamtlösung.
3. Ein Modeler klingt schlecht!
Das muß allerdings nicht so sein. Der zu treibende Entwicklungsaufwand ist jedoch nicht unerheblich und kann in der Regel nur von Elektroingenieuren geleistet werden. Dementsprechend entstehen hier hohe Kosten. Damit dürfte auch klar geworden sein, warum die billigen Modeler tatsächlich schlecht klingen. Man hat aus Zeit- und Kostengründen einfach nicht sorgfältig genug gearbeitet und quasi die Hälfte vergessen!
Zusammenfassung
Mit Hilfe der Methoden der digitalen Signalverarbeitung läßt sich ein analoger Verstärker vollständig nachbilden (Gleiches gilt übrigens auch für die Modellierung von Effekten).
Die Qualität und damit das klangliche Ergebnis steht und fällt mit der Qualität der verwendeten analogen Modelle des zu modellierenden Verstärkers.
Ulf
