Man nimmt seine Gitarre zur Hand, schlägt eine Saite an und hört...
...und was man da hört, kann ganz unterschiedlich sein.
Jeder Elektrogitarrist weiß, daß zwischen dem verstärkten Klang der Gitarre und ihrem akustischen Klang Welten liegen. Es stellt sich die Frage, ob das nur an den Übertragungseigenschaften von Tonabnehmer, Elektronik und Lautsprecher liegt oder ob da noch mehr im Spiel ist? Muß das klangliche Ergebnis nicht gleich sein, wenn man den Klang mit einem guten Mikrofon abnimmt und dann auf den Verstärker gibt?
Die Antwort auf diese Fragen findet man, wenn man die Funktionsprinzipien von E- und A-Gitarre einmal gegenüberstellt.
Sehen wir uns einmal die Übertragungskette der Instrumente an:
1. Am Anfang ist die Naturtonreihe
Den Anfang unserer Kette macht eine theoretische Konstruktion: Eine Quelle, die einen Grundton f0 und seine ganzzahligen Vielfachen mit gleichen Amplituden erzeugt. Es gilt dann
yn(t)=sin(2*pi*[n+1]*f0*t)
Für das gesamte Schallereignis gilt dann
y(t)=y0(t)+y1(t)+y2(t)+...yn(t)
wobei n von 0 bis Unendlich läuft. Ich möchte diese Quelle einmal als Naturtonquelle bezeichnen.
Eine solche Schallquelle gibt es in der Natur natürlich nicht, aber als Quelle eine Modells für die Gitarre (und auch für alle anderen Schallerzeuger) ist sie sehr gut geeignet.
2. Wo man hinlangt...
...spielt schon eine Rolle. Je nach dem an welcher Position man die Saite anschlägt, verändert sich der Klang. Dabei gilt: Je weiter vom Steg entfernt in Richtung 12. Bund desto voller der Klang. Darüber hinaus ergibt sich aus der Anschlagposition auch ein Kammfiltereffekt, der einzelne Harmonische und deren Vielfache teilweise total auslöschen kann. Hier ein Beispiel für ein Filter, daß mit der Naturtonquelle gespeist wurde:
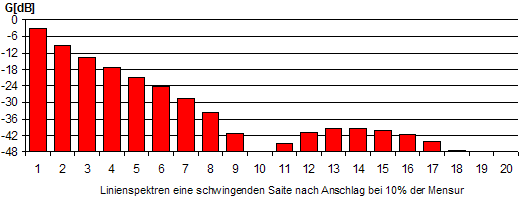
Man erkennt, daß die 10. und 20. Harmonische vollständig fehlen. Bei eine Position von 25% wären es dann die 4., 8., 12., usw.
3. Die Saite ist ein Filter...
Man kann jede Saite als ein Filter auffassen, welches bestimmte Frequenzen dämpft und andere wiederum betont. Es existieren also Resonanzen und Antiresonanzen. Die Lage dieser Resonanzen wird durch den Aufbau und die materielle Komposition der Saite bestimmt. Auch ihre Zugspannung dürfte hier eine Rolle spielen.
Darüber hinaus hat jede Saite auch zwei Tiefpaßcharakteristiken. Die eine wird wieder von Material und Aufbau bestimmt, die zweite hängt vom Alter und der Verschmutzung ab. Ihre Grenzfrequenz rutscht mit zunehmender Alterung nach unten. Also: Alte Saite=dumpf!
Dieses sehr komplizierte Filter generiert aus unserer Naturtonquelle den Klang der Saite. Würde die Saite dämpfungsarm aufgehängt und wären die beiden Aufhängungspunkte nicht miteinander verbunden. So wäre das exakt der Klang, den wir hören könnten.
4. Verstärkung tut Not
Eine schwingende Saite zählt nun nicht gerade zu den besonders lauten Schallerzeugern. Im Laufe der Geschichte wurden dann Dinge dazugebaut, die nur einen Zweck hatte: Das Schallereignis zu verstärken!
4.1 Die Akustische macht's mechanisch
Der Korpus einer guten akustischen Gitarre erfüllt diese Aufgabe in der Regel sehr gut. Die Energie der Saitenschwingung wird über die Aufhängung (Steg und Sattel) auf den Korpus übertragen. Dieser gerät nun seinerseits in Schwingungen und seine Oberfläche wirkt wie die Membran eines Lautsprechers, welche die mechanische Energie in Schallenergie umwandelt. Der Korpus entzieht also den Saiten die Schwingungsenergie und es ist in der Theorie sogar denkbar, daß die Saitenschwingung schon abgeklungen ist, der Korpus aber noch nachschwingt.
Der Korpus selber verfügt ebenfalls über Resonanzen und Antiresonanzen. Die Fähigkeit die mechanische Energie der Saitenschwingung zu übernehmen, kann durch die sogenannte mechanische Konduktanz beschrieben werden. Letztendlich kann man sich Korpus und Hals mit den mechanischen Beschlägen ebenfalls als (sehr komplexes) Filter denken.
4.2 Elektriktrick
Eine Elektrogitarre schöpft ihr fast unendliches Lautstärkepotential aus einem elektronischen Verstärker mit Lautsprecher. Bevor der jedoch arbeiten kann, muß die Saitenschwingung in ein elektrisches Signal umgewandelt werden. Diese Aufgabe übernimmt in der Regel ein elektromagnetischer Tonabnehmer, welcher direkt unter den Saiten positioniert wird.
5. Der Raum nimmt Einfluß
Bevor die von einer Quelle ausgesendeten Schallwellen im Ohr des Zuhörers ankommen, müssen sie sich durch den Raum ausbreiten. Aus Sicht des Zuhörers muß man dabei zwischen direktem und indirektem Schall unterscheiden.
Schallwellen breiten sich grundsätzlich nur gradlinig aus. Der direkte Schall bewegt sich, wie der Name schon andeutet, direkt - das heißt auf dem kürzesten Weg - von der Quelle zum Zuhörer. Schallwellen, die eine andere Richtung nehmen, erreichen den Zuhörer normalerweise nicht. Treffen sie jedoch auf ein Hindernis, wie zum Beispiel eine Wand, so werden die Wellen nach dem Reflektionsgesetzt reflektiert. Dabei können auch frequenzabhängige Dämpfungen auftreten, die abhängig von den Materialien dieser Hindernisse sind. Das Hindernis wirkt dabei auch als Filter und es entsteht eine Klangumformung. Auf diese Weise wird der Schall quasi umgeleitet und kann so doch noch - wenn auch indirekt - zum Zuhörer gelangen.
Hier ist jetzt auch eine Besonderheit des indirekten Schalls zu erkennen: Bedingt durch den längeren Weg, ist dieser Schall um die Wegdifferenz verzögert, die wir als Echo wahrnehmen. Da sich der Schall vom Korpus ausgehend in alle Richtungen ausbreitet, treten in einem Raum eine Vielzahl von unterschiedlichen Verzögerungen auf, die alle mit einem eigenen Filter bewertet sind. Mehrfachreflektionen sind dabei nicht ungewöhnlich.
Neben diesem Effekt treten beim Empfänger - dem Zuhörer - auch noch Auslöschungen oder Verstärkungen der Schallwellen auf, die durch die unterschiedlichen Laufzeiten der verschiedenen Wellen entstehen. Die Summe dieser Verzögerungen mit ihren klangumformenden Wirkungen versetzt uns in die Lage, aus dem Gehörten auf die Raumgröße und -ausstattung zu schließen. Diese Vielzahl von quasi diffusen Echos wird auch als Hall bezeichnet und stellt ein Charakteristikum für den jeweiligen Raum dar. Der Raum ändert also den Klang, welcher von der Quelle abgestrahlt wird.
Zusätzlich zu den eben festgestellten Eigenschaften, ist das klangliche Empfinden auch noch von der Position des Zuhörers im Raum abhängig. Wird sie verändert, so ändern sich auch die Laufzeiten und Klangumformungen der empfangenen Schallwellen. Es ist daher sehr wohl möglich, daß zwei Menschen in einem Raum aufgrund verschiedener Hörpositionen den Klang unterschiedlich empfinden. Die akustischen Eigenschaften eines Raumes sind also sehr komplex und haben einen maßgeblichen Einfluß auf die Klangentstehung.
6 Das Ohr als Filter
Das menschliche Ohr ist vom Prinzip her so ausgelegt, daß es Frequenzen bis 25kHz empfangen kann. Diese Bandbreite ist jedoch vom Alter abhängig. Während Säuglinge noch über die volle Bandbreite verfügen, hören 20 bis 30jährige selten mehr als 18kHz. Alte Menschen müssen manchmal sogar mit 10kHz oder weniger auskommen. In diese Kategorie muß man auch den einen oder anderen (noch jungen) Musiker einordnet, dem der Marshall-Turm schon in frühen Jahren das Gehör "weggepustet" hat. Unser Ohr stellt damit ein Tiefpaßsystem dar, dessen Grenzfrequenz eine Funktion des Alters ist.
Das gleiche akustische Ereignis wird von zwei unterschiedlich alten Hörern folglich verschieden wahrgenommen. Damit ist schon die erste Begründung dafür geliefert, warum Menschen einen Klang unterschiedlich empfinden.
Das menschliche Ohr hat jedoch noch eine weitere interessante Eigenschaft: Seine Empfindlichkeit. Das nächste Bild zeigt einen typischen Verlauf:
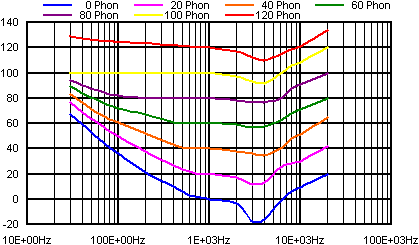
Die Empfindlichkeitskurve des menschlichen Gehörs
Die Kurven geben an, welcher Schallpegel (hier in dB) in Abhängigkeit der Frequenz im menschlichen Ohr den gleichen Lautstärkeeindruck erzeugt. Bei 30 Hz liegt die Hörschwelle (0 Phon) bei einem Schallpegel von 67 dB. Bei 1 kHz nimmt das Ohr schon Pegel von 0 dB wahr. Seine größte Empfindlichkeit liegt in etwa bei 3 kHz. Die Schmerzschwelle von 120 Phon zeigt die obere Kurve. Auch hier ist noch ein frequenzabhängiges Verhalten zu erkennen.
Es fällt auf, daß der Verlauf der einzelnen Lautstärkeschwellen unterschiedlich ist. Daraus folgt, daß ein und dasselbe akustische Ereignis in Abhängigkeit seiner Lautstärke als unterschiedlicher Klang wahrgenommen wird. Tatsächlich empfinden wir den Klang einer lauten Elektrogitarre als "voller". Es scheint, als ob mehr tiefe und hohe Töne vorhanden sind.
Um dieses Verhalten zu kompensieren, wird in der HiFi-Technik die sogenannte gehörrichtige Lautstärkeeinstellung (Loudness) benutzt. Bei kleinen Lautstärken werden die hohen und tiefen Frequenzen mehr betont. Auf diese Weise wird die Hörkurve kompensiert und man erhält bei jeder Lautstärke in etwa einen vergleichbaren Klangeindruck.
7 Das programierte Gehör - unser Gehirn
Neben diesen meßbaren Effekten sind noch ein paar psychologische Einflüsse zu verzeichnen, die böse Zungen auch als Einbildung bezeichen würden. Diese Effekte sind jedoch immer mit zusätzlichen visuellen Reizen verbunden. Dazu stellen wir uns eine kleines Gedankenexperiment in einem Musikgeschäft vor:
Unserem Probanden werden zwei gleiche Gitarren gleichen Typs (Les Paul, um ein Beispiel zu nennen) präsentiert, die von unterschiedlichen Herstellern stammen. Wir setzen dabei voraus, daß für beiden Instrumente das gleiche Material verwendet wurde, sie also im weitesten Sinne als identisch oder vergleichbar zu bezeichnen sind. Der eine Hersteller heißt natürlich "Gibson" (wie könnte es anders sein?), der andere ist eine unbekannte Firma aus Asien, deren Produkt um die Hälfte billiger ist.
Nun werden beide Instrumente vom selben Musiker an einem identischen Setup vorgeführt. Für welches Instrument wird sich unser Kandidat wohl entscheiden?
"Natürlich klingt die Gibson besser!", wird er vermutlich mit dem Brustton der Überzeugung sagen und damit schnell seine Wahl treffen. Aber ist diese Wahl wirklich objektiv?
Auch wenn beide Instrumente wirklich einen identischen Klang abliefern, hat das No-Name-Produkt schlechte Karten, denn nur Gibson baut gute Gitarren, wie man es immer zu hören und zu lesen bekommt und gute Gitarre haben auch immer einen hohen Preis. Hätte man diesen Test mit verbundenen Augen gemacht und nicht die Herstellernamen und Preise genannt, so wäre der Ausgang des Experimentes völlig offen gewesen. Manchmal hören wir eben das, was wir hören wollen. Besonders, wenn unsere Meinung zu einem Thema durch geeignete suggestive Werbemaßnahmen in gewisser Weise "programmiert" wurde.
8 Rückkopplungen durch den Raum
Jeder Gitarrist weiß, daß ab einer bestimmten Lautstärke ein Effekt einsetzt, der als Rückkopplung bezeichnet wird. Dabei regen die Schallwellen die Saiten und den Korpus der Gitarre zum Schwingen an. Im schlechtesten Fall ist auch der Tonabnehmer mikrofonisch und die Drahtwindungen beginnen ebenfalls zu schwingen. Die Gitarre beginnt zu "leben" und tritt über den Raum in Wechselwirkung mit dem Lautsprecher.
Im besten (oder lautesten) Fall bildet sich eine konstante Schwingung mit maximaler Lautstärke aus und man spricht von einer Mitkopplung. Wann und bei welcher Frequenz das geschieht, ist unter anderem von den akustischen Eigenschaften des Raumes und von der Position der Gitarre im Raum abhängig. Bedingt durch die verschiedenen Laufzeiten der Schallwellen können sich dabei sowohl Gegen- als auch Mitkopplungen ergeben. Sie verringern oder verstärken bestimmte Frequenzen selektiv.
Die Wirkung dieser Rückkopplung ist grundsätzlich vorhanden. Der tatsächlich Einfluß steigt mit der Lautstärke.
9 Akustik vs. Elektrik
Auch wenn man es auf den ersten Blick nicht glauben mag, bestehen zwischen der Klangverarbeitung von Elektro- und Akustikgitarre große Unterschiede. Betrachten wir zunächst einmal die Klangkette einer Akustikgitarre:

Die Klangkette der akustischen Gitarre
Unmittelbar nach der Naturtonquelle kommt ein Kammfilter, deren Kammfrequenzen durch die Anschlagposition bestimmt werden. Danach folgt das Saitenfilter mit seinen spezifischen Resonanzen und den beiden Tiefpaßcharakteristiken. Anschließend gelangt das Signal in den Korpus, der ein weiteres Filter darstellt. Da er der Saite die Schwingungsenergie entzieht, wurde eine Rückführung auf den Eingang des Saitenfilters vorgesehen. Aufgrund des negativen Vorzeichens an der Additionsstelle handelt es sich aus technischer Sicht um eine sogenannte Gegenkopplung.
Wird der Schall des Korpus durch ein Mikrofon oder einen Piezowandler abgenommen, so kommt noch ein elektronischer Block mit Verstärker, Effektgeräten und Lautsprecher hinzu. Da sie nicht zwingend vorhanden sein müssen, wurden sie gestrichelt dargestellt.
Vom Lautsprecher gelangt der Schall dann wieder über den Raum zum Instrument zurück. Je nach räumlicher Anordnung von Instrument und Lautsprecher kann diese Rückführung einen Gegen- oder Mitkopplung sein. Im letzteren Fall besteht die Gefahr einer sich aufbauenden Schwingung mit maximaler Lautstärke (Rückkopplung), welche im Extremfall zur Zerstörung des Instrumentes führen kann. Diese Rückkopplung hat bei der akustischen Gitarre natürlich den größten Einfluß auf den Korpus, da er sich aufgrund seiner Konstruktion leicht zum Schwingen anregen läßt.
Kommen wir jetzt zur Elektrogitarre. Auf den ersten Blick sieht die Klangkette recht ähnlich aus. Wenn man jedoch genauer hinsieht, so offenbaren sich wesentliche Unterschiede, auf die ich im folgenden eingehen möchte. Zur besseren Übersicht wurden die Blöcke der Akustikgitarre in blau dargestellt.
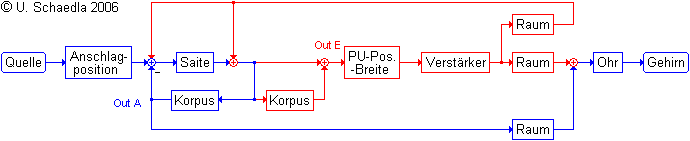
Die Klangkette der elektrischen Gitarre
Es fällt auf, daß hier zwei mit "Korpus" bezeichnete Filter existieren. Die Begründung dafür ist einfach: Wenn der Korpus schwingt, geraten auch die Tonabnehmer in Schwingungen. Es ändert sich dann der Abstand zwischen Tonabnehmer und Saite, was eine Induktionsspannung zur Folge hat. Dieser Effekt ist bei einer massiven Korpuskonstruktion sicherlich nicht besonders erwähnenswert. Bei einer Jazzgitarre mit einer frei schwingenden Decke mag es da schon anders aussehen. Ob das Signal aus diesem Korpusfilter zur Saitenschwingung addiert oder subtrahiert wird, hängt unter anderem vom Ruheabstand des Tonabnehmers zu den Saiten ab. Vermutlich wird die Phasenlage von der Frequenz abhängen, sodas beide Möglichkeiten auftreten können.
Nach der Additionsstelle folgt ein weiteres Kammfilter, dessen Kammfrequenzen sowohl von der Position des Tonabnehmers als auch von seiner magnetischen Breite (Apertur) abhängig ist. Die unterschiedlichen Klänge der einzelnen Tonabnehmerpositionen (z.B. bei der Strat) werden maßgeblich durch dieses Filter bestimmt. Wohlgemerkt handelt es sich hierbei nicht um ein elektronisches Filter. Die elektrischen Eigenschaften des Tonabnehmers spielen hier also keinerlei Rolle!
Die folgenden Bestandteile wie Verstärker und Raum nebst Rückkopplung wurden bereits bei der Klangkette der akustischen Gitarre beschrieben. Hier ist lediglich zu bemerken, daß im Verstärkerblock auch die elektrische Wirkungen des Tonabnehmers und der Gitarrenelektronik enthalten sind.
Soweit eigentlich nicht Neues. Der eigentliche Unterschied erschließt sich einem nur, wenn man die Lage der beiden "Ausgänge" betrachtet. Sie wurden mit "Out A" und "Out E" bezeichnet. Wenn man die wesentlichen mechanischen Elemente der Klangkette neu ordnet, kommt man zum folgenden Bild:
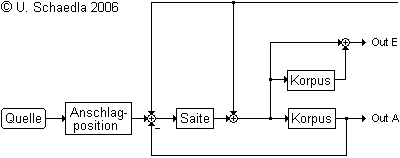
Akustischer (A) und elektrischer (E) Signalausgang einer Gitarre
Man erkennt, daß die beiden Signale E und A in gewisser Weise komplementär sind. Um diese Vermutung etwas genauer zu beleuchten, machen wir ein paar Vereinfachungen:
1. Wir vernachlässigen die Rückkopplung durch den Raum und
2. wir vernachlässigen den Einfluß der Korpusschwingung auf den Tonabnehmerabstand.
Dadurch entfallen zwei Additionsstellen und ein Korpusblock. Jetzt noch ein Trick aus der Systemtechnik (Verschiebung des verbleibenden Korpusfilters hinter die Verzweigung) und wir erhalten ein recht einfaches Modell:
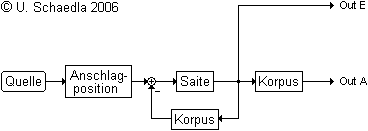
Vereinfachtes Modell der Signalausgänge einer Gitarre
Wer mit der Systemtheorie und Wirkungsplänen vertraut ist, der kann jetzt ein wenig rechnen: Unter der Annahme, daß das Signal der Quelle In(s) ist lassen sich für beide Ausgänge jeweils eine Übertragungsfunktion (1), (2) angeben:
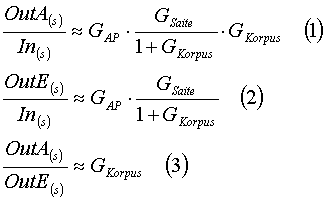
Verschiedene mechanische Übertragungsfunktionen der Gitarre
Besonders interessant ist jetzt das Verhältnis von Akustik zu Elektrik (3). Es wird einzig von den Übertragungseigenschaften des Korpus bestimmt!
Aus diesen drei Formel kann man folgende allgemeine Schlußfolgerung ziehen:
Die akustische Gitarre liefert den durch den Korpus betonten Teil der Saitenschwingung und die Elektrogitarre liefert den Teil, der nicht durch den Korpus betont wird.
Die ideale Elektrogitarre hätte folglich eine nichtschwingfähigen Korpus. Er soll nicht resonieren, um die Saitenschwingung nicht zu dämpfen. Die entprechende Übertragungsfunktion GKorpus hätte folglich bei allen Frequenzen einen Wert von 0!
In der Folge wäre das akustische Signal
OutA=0
und
OutE=GAP*GSaite*In
Der starre Korpus einer Elektrogitarre liefert auch die Erklärung für das, im Vergleich zur Akustikgitarre, lange Sustain. Die Saitenschwingung muß eben keine (oder nur wenig) Energie an den Korpus abgeben und kann so länger schwingen.
Ein maximal schwingfähiger Korpus für eine Akustikgitarre hätte eine Übertragungsfunktion mit einem unendlichen Wert. Dann wird
OutE=0
und
OutA=GAP*GSaite*In
Die beiden extremen Anforderungen an den Korpus finden seinen Niederschlag in Konstruktion und Materialauswahl. Man wird kaum eine Akustikgitarre finden, deren Korpus aus den klassischen Korpushölzern einer Elektrogitarre (Mahagoni, Ahorn, Esche, Erle) gebaut wurde. Statt dessen wird hier gerne Fichte, Palisander und teilweise Ahorn verwendet.
Der Bau eines guten Resonanzkorpus ist in der Tat eine Meisterleistung, die nur wenige wirklich beherrschen. Einen massiven Korpus für eine Elektrogitarre hingegen kann jeder Tischler zusammenschustern, so er denn ein ordentliches Tonholz ausgewählt hat.
10 Fazit
Wer schon einmal versucht hat, eine Westerngitarre mit einem elektromagnetischen Tonabnehmer auszurüsten, der wird vom Ergebnis in der Regel enttäuscht gewesen sein. Warum das so sein muß, dürfte jetzt klar geworden sein. Statt des gewünschten OutA übertragen wir OutE, welches darüber hinaus noch mit einem zusätzlichen Kammfilter (Position und Breite) und der elektrischen Filterwirkung des Tonabnehmers bewertet wurde. Es klingt dann eben immer ein wenig "elektrisch".
Seit einiger Zeit gibt es für Elektrogitarren sogenannte Akustiksimulatoren, die entweder als kleiner Bodentreter oder als Effekt in einem Verstärker verfügbar sind. Wenn man sich die Ergebnisse unserer Überlegungen ansieht wird klar, daß diese kleinen Kisten ganz große Lügner sind.
Hochwertige Exemplare simulieren zwar den Korpus, sodas gilt
OutA'=OutE*G'Korpus*In
aber der störende Einfluß von Kammfilter und Tonabnehmer bleibt. Darüber hinaus spielt auch noch der Eigenklang des Gitarrenkorpus eine Rolle. Eine geeignete Kompensation, welche für jede E-Gitarre optimal ist, wird man nicht realisieren können. Das Ergebnis dieses "Fakes" bleibt also ein mehr oder weniger guter Kompromiß!
Wer also den akustischen Klang verstärken möchte, kommt nicht umhin, die mechanische Schwingung des Korpus durch einen geeigneten Sensor in eine elektrischen Spannung umzuwandeln.
Einige Elektrogitarren verfügen, neben den elektromagnetischen Tonabnehmern, auch noch über piezoelektrische Sensoren. Sie sind dann tatsächlich in der Lage, das akustische Signal zu übertragen. Allerdings darf man hier nicht vergessen, daß zwischen den Übertragungseigenschaften eines massiven E-Gitarrenkorpus und einem Resonanzkorpus einer Akustikgitarre Welten liegen. Eine Elektrogitarre ist eben darauf optimiert OutE zu maximieren, was automatisch zu einer Verringerung von OutA führt. Der akustische Klang einer massiven Les Paul ist also keinesfalls mit dem einer ordentlichen Westerngitarre zu vergleichen.
Akustische Gitarren mit eingebauten Tonabnehmern oder Mikrofonen sind klanglich auch nicht immer überzeugend, denn um die Anfälligkeit für Rückkopplungen zu senken, wird ein solcher Korpus immer etwas steifer konstruiert. So richtig "voll" und "satt" klingen solche Instrumente dann nicht. Dieses fehlende Etwas läßt sich dann am Verstärker zufügen, sodas insgesamt schon ein gutes Ergebnis entstehen kann.
Ulf
(Die korrigierte und erweiterte Version dieses Artikels findet sich in der Knowledge-Base der Guitar-Letter)
...und was man da hört, kann ganz unterschiedlich sein.
Jeder Elektrogitarrist weiß, daß zwischen dem verstärkten Klang der Gitarre und ihrem akustischen Klang Welten liegen. Es stellt sich die Frage, ob das nur an den Übertragungseigenschaften von Tonabnehmer, Elektronik und Lautsprecher liegt oder ob da noch mehr im Spiel ist? Muß das klangliche Ergebnis nicht gleich sein, wenn man den Klang mit einem guten Mikrofon abnimmt und dann auf den Verstärker gibt?
Die Antwort auf diese Fragen findet man, wenn man die Funktionsprinzipien von E- und A-Gitarre einmal gegenüberstellt.
Sehen wir uns einmal die Übertragungskette der Instrumente an:
1. Am Anfang ist die Naturtonreihe
Den Anfang unserer Kette macht eine theoretische Konstruktion: Eine Quelle, die einen Grundton f0 und seine ganzzahligen Vielfachen mit gleichen Amplituden erzeugt. Es gilt dann
yn(t)=sin(2*pi*[n+1]*f0*t)
Für das gesamte Schallereignis gilt dann
y(t)=y0(t)+y1(t)+y2(t)+...yn(t)
wobei n von 0 bis Unendlich läuft. Ich möchte diese Quelle einmal als Naturtonquelle bezeichnen.
Eine solche Schallquelle gibt es in der Natur natürlich nicht, aber als Quelle eine Modells für die Gitarre (und auch für alle anderen Schallerzeuger) ist sie sehr gut geeignet.
2. Wo man hinlangt...
...spielt schon eine Rolle. Je nach dem an welcher Position man die Saite anschlägt, verändert sich der Klang. Dabei gilt: Je weiter vom Steg entfernt in Richtung 12. Bund desto voller der Klang. Darüber hinaus ergibt sich aus der Anschlagposition auch ein Kammfiltereffekt, der einzelne Harmonische und deren Vielfache teilweise total auslöschen kann. Hier ein Beispiel für ein Filter, daß mit der Naturtonquelle gespeist wurde:

Man erkennt, daß die 10. und 20. Harmonische vollständig fehlen. Bei eine Position von 25% wären es dann die 4., 8., 12., usw.
3. Die Saite ist ein Filter...
Man kann jede Saite als ein Filter auffassen, welches bestimmte Frequenzen dämpft und andere wiederum betont. Es existieren also Resonanzen und Antiresonanzen. Die Lage dieser Resonanzen wird durch den Aufbau und die materielle Komposition der Saite bestimmt. Auch ihre Zugspannung dürfte hier eine Rolle spielen.
Darüber hinaus hat jede Saite auch zwei Tiefpaßcharakteristiken. Die eine wird wieder von Material und Aufbau bestimmt, die zweite hängt vom Alter und der Verschmutzung ab. Ihre Grenzfrequenz rutscht mit zunehmender Alterung nach unten. Also: Alte Saite=dumpf!
Dieses sehr komplizierte Filter generiert aus unserer Naturtonquelle den Klang der Saite. Würde die Saite dämpfungsarm aufgehängt und wären die beiden Aufhängungspunkte nicht miteinander verbunden. So wäre das exakt der Klang, den wir hören könnten.
4. Verstärkung tut Not
Eine schwingende Saite zählt nun nicht gerade zu den besonders lauten Schallerzeugern. Im Laufe der Geschichte wurden dann Dinge dazugebaut, die nur einen Zweck hatte: Das Schallereignis zu verstärken!
4.1 Die Akustische macht's mechanisch
Der Korpus einer guten akustischen Gitarre erfüllt diese Aufgabe in der Regel sehr gut. Die Energie der Saitenschwingung wird über die Aufhängung (Steg und Sattel) auf den Korpus übertragen. Dieser gerät nun seinerseits in Schwingungen und seine Oberfläche wirkt wie die Membran eines Lautsprechers, welche die mechanische Energie in Schallenergie umwandelt. Der Korpus entzieht also den Saiten die Schwingungsenergie und es ist in der Theorie sogar denkbar, daß die Saitenschwingung schon abgeklungen ist, der Korpus aber noch nachschwingt.
Der Korpus selber verfügt ebenfalls über Resonanzen und Antiresonanzen. Die Fähigkeit die mechanische Energie der Saitenschwingung zu übernehmen, kann durch die sogenannte mechanische Konduktanz beschrieben werden. Letztendlich kann man sich Korpus und Hals mit den mechanischen Beschlägen ebenfalls als (sehr komplexes) Filter denken.
4.2 Elektriktrick
Eine Elektrogitarre schöpft ihr fast unendliches Lautstärkepotential aus einem elektronischen Verstärker mit Lautsprecher. Bevor der jedoch arbeiten kann, muß die Saitenschwingung in ein elektrisches Signal umgewandelt werden. Diese Aufgabe übernimmt in der Regel ein elektromagnetischer Tonabnehmer, welcher direkt unter den Saiten positioniert wird.
5. Der Raum nimmt Einfluß
Bevor die von einer Quelle ausgesendeten Schallwellen im Ohr des Zuhörers ankommen, müssen sie sich durch den Raum ausbreiten. Aus Sicht des Zuhörers muß man dabei zwischen direktem und indirektem Schall unterscheiden.
Schallwellen breiten sich grundsätzlich nur gradlinig aus. Der direkte Schall bewegt sich, wie der Name schon andeutet, direkt - das heißt auf dem kürzesten Weg - von der Quelle zum Zuhörer. Schallwellen, die eine andere Richtung nehmen, erreichen den Zuhörer normalerweise nicht. Treffen sie jedoch auf ein Hindernis, wie zum Beispiel eine Wand, so werden die Wellen nach dem Reflektionsgesetzt reflektiert. Dabei können auch frequenzabhängige Dämpfungen auftreten, die abhängig von den Materialien dieser Hindernisse sind. Das Hindernis wirkt dabei auch als Filter und es entsteht eine Klangumformung. Auf diese Weise wird der Schall quasi umgeleitet und kann so doch noch - wenn auch indirekt - zum Zuhörer gelangen.
Hier ist jetzt auch eine Besonderheit des indirekten Schalls zu erkennen: Bedingt durch den längeren Weg, ist dieser Schall um die Wegdifferenz verzögert, die wir als Echo wahrnehmen. Da sich der Schall vom Korpus ausgehend in alle Richtungen ausbreitet, treten in einem Raum eine Vielzahl von unterschiedlichen Verzögerungen auf, die alle mit einem eigenen Filter bewertet sind. Mehrfachreflektionen sind dabei nicht ungewöhnlich.
Neben diesem Effekt treten beim Empfänger - dem Zuhörer - auch noch Auslöschungen oder Verstärkungen der Schallwellen auf, die durch die unterschiedlichen Laufzeiten der verschiedenen Wellen entstehen. Die Summe dieser Verzögerungen mit ihren klangumformenden Wirkungen versetzt uns in die Lage, aus dem Gehörten auf die Raumgröße und -ausstattung zu schließen. Diese Vielzahl von quasi diffusen Echos wird auch als Hall bezeichnet und stellt ein Charakteristikum für den jeweiligen Raum dar. Der Raum ändert also den Klang, welcher von der Quelle abgestrahlt wird.
Zusätzlich zu den eben festgestellten Eigenschaften, ist das klangliche Empfinden auch noch von der Position des Zuhörers im Raum abhängig. Wird sie verändert, so ändern sich auch die Laufzeiten und Klangumformungen der empfangenen Schallwellen. Es ist daher sehr wohl möglich, daß zwei Menschen in einem Raum aufgrund verschiedener Hörpositionen den Klang unterschiedlich empfinden. Die akustischen Eigenschaften eines Raumes sind also sehr komplex und haben einen maßgeblichen Einfluß auf die Klangentstehung.
6 Das Ohr als Filter
Das menschliche Ohr ist vom Prinzip her so ausgelegt, daß es Frequenzen bis 25kHz empfangen kann. Diese Bandbreite ist jedoch vom Alter abhängig. Während Säuglinge noch über die volle Bandbreite verfügen, hören 20 bis 30jährige selten mehr als 18kHz. Alte Menschen müssen manchmal sogar mit 10kHz oder weniger auskommen. In diese Kategorie muß man auch den einen oder anderen (noch jungen) Musiker einordnet, dem der Marshall-Turm schon in frühen Jahren das Gehör "weggepustet" hat. Unser Ohr stellt damit ein Tiefpaßsystem dar, dessen Grenzfrequenz eine Funktion des Alters ist.
Das gleiche akustische Ereignis wird von zwei unterschiedlich alten Hörern folglich verschieden wahrgenommen. Damit ist schon die erste Begründung dafür geliefert, warum Menschen einen Klang unterschiedlich empfinden.
Das menschliche Ohr hat jedoch noch eine weitere interessante Eigenschaft: Seine Empfindlichkeit. Das nächste Bild zeigt einen typischen Verlauf:

Die Empfindlichkeitskurve des menschlichen Gehörs
Die Kurven geben an, welcher Schallpegel (hier in dB) in Abhängigkeit der Frequenz im menschlichen Ohr den gleichen Lautstärkeeindruck erzeugt. Bei 30 Hz liegt die Hörschwelle (0 Phon) bei einem Schallpegel von 67 dB. Bei 1 kHz nimmt das Ohr schon Pegel von 0 dB wahr. Seine größte Empfindlichkeit liegt in etwa bei 3 kHz. Die Schmerzschwelle von 120 Phon zeigt die obere Kurve. Auch hier ist noch ein frequenzabhängiges Verhalten zu erkennen.
Es fällt auf, daß der Verlauf der einzelnen Lautstärkeschwellen unterschiedlich ist. Daraus folgt, daß ein und dasselbe akustische Ereignis in Abhängigkeit seiner Lautstärke als unterschiedlicher Klang wahrgenommen wird. Tatsächlich empfinden wir den Klang einer lauten Elektrogitarre als "voller". Es scheint, als ob mehr tiefe und hohe Töne vorhanden sind.
Um dieses Verhalten zu kompensieren, wird in der HiFi-Technik die sogenannte gehörrichtige Lautstärkeeinstellung (Loudness) benutzt. Bei kleinen Lautstärken werden die hohen und tiefen Frequenzen mehr betont. Auf diese Weise wird die Hörkurve kompensiert und man erhält bei jeder Lautstärke in etwa einen vergleichbaren Klangeindruck.
7 Das programierte Gehör - unser Gehirn
Neben diesen meßbaren Effekten sind noch ein paar psychologische Einflüsse zu verzeichnen, die böse Zungen auch als Einbildung bezeichen würden. Diese Effekte sind jedoch immer mit zusätzlichen visuellen Reizen verbunden. Dazu stellen wir uns eine kleines Gedankenexperiment in einem Musikgeschäft vor:
Unserem Probanden werden zwei gleiche Gitarren gleichen Typs (Les Paul, um ein Beispiel zu nennen) präsentiert, die von unterschiedlichen Herstellern stammen. Wir setzen dabei voraus, daß für beiden Instrumente das gleiche Material verwendet wurde, sie also im weitesten Sinne als identisch oder vergleichbar zu bezeichnen sind. Der eine Hersteller heißt natürlich "Gibson" (wie könnte es anders sein?), der andere ist eine unbekannte Firma aus Asien, deren Produkt um die Hälfte billiger ist.
Nun werden beide Instrumente vom selben Musiker an einem identischen Setup vorgeführt. Für welches Instrument wird sich unser Kandidat wohl entscheiden?
"Natürlich klingt die Gibson besser!", wird er vermutlich mit dem Brustton der Überzeugung sagen und damit schnell seine Wahl treffen. Aber ist diese Wahl wirklich objektiv?
Auch wenn beide Instrumente wirklich einen identischen Klang abliefern, hat das No-Name-Produkt schlechte Karten, denn nur Gibson baut gute Gitarren, wie man es immer zu hören und zu lesen bekommt und gute Gitarre haben auch immer einen hohen Preis. Hätte man diesen Test mit verbundenen Augen gemacht und nicht die Herstellernamen und Preise genannt, so wäre der Ausgang des Experimentes völlig offen gewesen. Manchmal hören wir eben das, was wir hören wollen. Besonders, wenn unsere Meinung zu einem Thema durch geeignete suggestive Werbemaßnahmen in gewisser Weise "programmiert" wurde.
8 Rückkopplungen durch den Raum
Jeder Gitarrist weiß, daß ab einer bestimmten Lautstärke ein Effekt einsetzt, der als Rückkopplung bezeichnet wird. Dabei regen die Schallwellen die Saiten und den Korpus der Gitarre zum Schwingen an. Im schlechtesten Fall ist auch der Tonabnehmer mikrofonisch und die Drahtwindungen beginnen ebenfalls zu schwingen. Die Gitarre beginnt zu "leben" und tritt über den Raum in Wechselwirkung mit dem Lautsprecher.
Im besten (oder lautesten) Fall bildet sich eine konstante Schwingung mit maximaler Lautstärke aus und man spricht von einer Mitkopplung. Wann und bei welcher Frequenz das geschieht, ist unter anderem von den akustischen Eigenschaften des Raumes und von der Position der Gitarre im Raum abhängig. Bedingt durch die verschiedenen Laufzeiten der Schallwellen können sich dabei sowohl Gegen- als auch Mitkopplungen ergeben. Sie verringern oder verstärken bestimmte Frequenzen selektiv.
Die Wirkung dieser Rückkopplung ist grundsätzlich vorhanden. Der tatsächlich Einfluß steigt mit der Lautstärke.
9 Akustik vs. Elektrik
Auch wenn man es auf den ersten Blick nicht glauben mag, bestehen zwischen der Klangverarbeitung von Elektro- und Akustikgitarre große Unterschiede. Betrachten wir zunächst einmal die Klangkette einer Akustikgitarre:

Die Klangkette der akustischen Gitarre
Unmittelbar nach der Naturtonquelle kommt ein Kammfilter, deren Kammfrequenzen durch die Anschlagposition bestimmt werden. Danach folgt das Saitenfilter mit seinen spezifischen Resonanzen und den beiden Tiefpaßcharakteristiken. Anschließend gelangt das Signal in den Korpus, der ein weiteres Filter darstellt. Da er der Saite die Schwingungsenergie entzieht, wurde eine Rückführung auf den Eingang des Saitenfilters vorgesehen. Aufgrund des negativen Vorzeichens an der Additionsstelle handelt es sich aus technischer Sicht um eine sogenannte Gegenkopplung.
Wird der Schall des Korpus durch ein Mikrofon oder einen Piezowandler abgenommen, so kommt noch ein elektronischer Block mit Verstärker, Effektgeräten und Lautsprecher hinzu. Da sie nicht zwingend vorhanden sein müssen, wurden sie gestrichelt dargestellt.
Vom Lautsprecher gelangt der Schall dann wieder über den Raum zum Instrument zurück. Je nach räumlicher Anordnung von Instrument und Lautsprecher kann diese Rückführung einen Gegen- oder Mitkopplung sein. Im letzteren Fall besteht die Gefahr einer sich aufbauenden Schwingung mit maximaler Lautstärke (Rückkopplung), welche im Extremfall zur Zerstörung des Instrumentes führen kann. Diese Rückkopplung hat bei der akustischen Gitarre natürlich den größten Einfluß auf den Korpus, da er sich aufgrund seiner Konstruktion leicht zum Schwingen anregen läßt.
Kommen wir jetzt zur Elektrogitarre. Auf den ersten Blick sieht die Klangkette recht ähnlich aus. Wenn man jedoch genauer hinsieht, so offenbaren sich wesentliche Unterschiede, auf die ich im folgenden eingehen möchte. Zur besseren Übersicht wurden die Blöcke der Akustikgitarre in blau dargestellt.

Die Klangkette der elektrischen Gitarre
Es fällt auf, daß hier zwei mit "Korpus" bezeichnete Filter existieren. Die Begründung dafür ist einfach: Wenn der Korpus schwingt, geraten auch die Tonabnehmer in Schwingungen. Es ändert sich dann der Abstand zwischen Tonabnehmer und Saite, was eine Induktionsspannung zur Folge hat. Dieser Effekt ist bei einer massiven Korpuskonstruktion sicherlich nicht besonders erwähnenswert. Bei einer Jazzgitarre mit einer frei schwingenden Decke mag es da schon anders aussehen. Ob das Signal aus diesem Korpusfilter zur Saitenschwingung addiert oder subtrahiert wird, hängt unter anderem vom Ruheabstand des Tonabnehmers zu den Saiten ab. Vermutlich wird die Phasenlage von der Frequenz abhängen, sodas beide Möglichkeiten auftreten können.
Nach der Additionsstelle folgt ein weiteres Kammfilter, dessen Kammfrequenzen sowohl von der Position des Tonabnehmers als auch von seiner magnetischen Breite (Apertur) abhängig ist. Die unterschiedlichen Klänge der einzelnen Tonabnehmerpositionen (z.B. bei der Strat) werden maßgeblich durch dieses Filter bestimmt. Wohlgemerkt handelt es sich hierbei nicht um ein elektronisches Filter. Die elektrischen Eigenschaften des Tonabnehmers spielen hier also keinerlei Rolle!
Die folgenden Bestandteile wie Verstärker und Raum nebst Rückkopplung wurden bereits bei der Klangkette der akustischen Gitarre beschrieben. Hier ist lediglich zu bemerken, daß im Verstärkerblock auch die elektrische Wirkungen des Tonabnehmers und der Gitarrenelektronik enthalten sind.
Soweit eigentlich nicht Neues. Der eigentliche Unterschied erschließt sich einem nur, wenn man die Lage der beiden "Ausgänge" betrachtet. Sie wurden mit "Out A" und "Out E" bezeichnet. Wenn man die wesentlichen mechanischen Elemente der Klangkette neu ordnet, kommt man zum folgenden Bild:

Akustischer (A) und elektrischer (E) Signalausgang einer Gitarre
Man erkennt, daß die beiden Signale E und A in gewisser Weise komplementär sind. Um diese Vermutung etwas genauer zu beleuchten, machen wir ein paar Vereinfachungen:
1. Wir vernachlässigen die Rückkopplung durch den Raum und
2. wir vernachlässigen den Einfluß der Korpusschwingung auf den Tonabnehmerabstand.
Dadurch entfallen zwei Additionsstellen und ein Korpusblock. Jetzt noch ein Trick aus der Systemtechnik (Verschiebung des verbleibenden Korpusfilters hinter die Verzweigung) und wir erhalten ein recht einfaches Modell:

Vereinfachtes Modell der Signalausgänge einer Gitarre
Wer mit der Systemtheorie und Wirkungsplänen vertraut ist, der kann jetzt ein wenig rechnen: Unter der Annahme, daß das Signal der Quelle In(s) ist lassen sich für beide Ausgänge jeweils eine Übertragungsfunktion (1), (2) angeben:
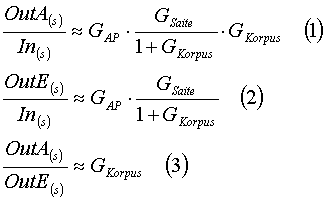
Verschiedene mechanische Übertragungsfunktionen der Gitarre
Besonders interessant ist jetzt das Verhältnis von Akustik zu Elektrik (3). Es wird einzig von den Übertragungseigenschaften des Korpus bestimmt!
Aus diesen drei Formel kann man folgende allgemeine Schlußfolgerung ziehen:
Die akustische Gitarre liefert den durch den Korpus betonten Teil der Saitenschwingung und die Elektrogitarre liefert den Teil, der nicht durch den Korpus betont wird.
Die ideale Elektrogitarre hätte folglich eine nichtschwingfähigen Korpus. Er soll nicht resonieren, um die Saitenschwingung nicht zu dämpfen. Die entprechende Übertragungsfunktion GKorpus hätte folglich bei allen Frequenzen einen Wert von 0!
In der Folge wäre das akustische Signal
OutA=0
und
OutE=GAP*GSaite*In
Der starre Korpus einer Elektrogitarre liefert auch die Erklärung für das, im Vergleich zur Akustikgitarre, lange Sustain. Die Saitenschwingung muß eben keine (oder nur wenig) Energie an den Korpus abgeben und kann so länger schwingen.
Ein maximal schwingfähiger Korpus für eine Akustikgitarre hätte eine Übertragungsfunktion mit einem unendlichen Wert. Dann wird
OutE=0
und
OutA=GAP*GSaite*In
Die beiden extremen Anforderungen an den Korpus finden seinen Niederschlag in Konstruktion und Materialauswahl. Man wird kaum eine Akustikgitarre finden, deren Korpus aus den klassischen Korpushölzern einer Elektrogitarre (Mahagoni, Ahorn, Esche, Erle) gebaut wurde. Statt dessen wird hier gerne Fichte, Palisander und teilweise Ahorn verwendet.
Der Bau eines guten Resonanzkorpus ist in der Tat eine Meisterleistung, die nur wenige wirklich beherrschen. Einen massiven Korpus für eine Elektrogitarre hingegen kann jeder Tischler zusammenschustern, so er denn ein ordentliches Tonholz ausgewählt hat.
10 Fazit
Wer schon einmal versucht hat, eine Westerngitarre mit einem elektromagnetischen Tonabnehmer auszurüsten, der wird vom Ergebnis in der Regel enttäuscht gewesen sein. Warum das so sein muß, dürfte jetzt klar geworden sein. Statt des gewünschten OutA übertragen wir OutE, welches darüber hinaus noch mit einem zusätzlichen Kammfilter (Position und Breite) und der elektrischen Filterwirkung des Tonabnehmers bewertet wurde. Es klingt dann eben immer ein wenig "elektrisch".
Seit einiger Zeit gibt es für Elektrogitarren sogenannte Akustiksimulatoren, die entweder als kleiner Bodentreter oder als Effekt in einem Verstärker verfügbar sind. Wenn man sich die Ergebnisse unserer Überlegungen ansieht wird klar, daß diese kleinen Kisten ganz große Lügner sind.
Hochwertige Exemplare simulieren zwar den Korpus, sodas gilt
OutA'=OutE*G'Korpus*In
aber der störende Einfluß von Kammfilter und Tonabnehmer bleibt. Darüber hinaus spielt auch noch der Eigenklang des Gitarrenkorpus eine Rolle. Eine geeignete Kompensation, welche für jede E-Gitarre optimal ist, wird man nicht realisieren können. Das Ergebnis dieses "Fakes" bleibt also ein mehr oder weniger guter Kompromiß!
Wer also den akustischen Klang verstärken möchte, kommt nicht umhin, die mechanische Schwingung des Korpus durch einen geeigneten Sensor in eine elektrischen Spannung umzuwandeln.
Einige Elektrogitarren verfügen, neben den elektromagnetischen Tonabnehmern, auch noch über piezoelektrische Sensoren. Sie sind dann tatsächlich in der Lage, das akustische Signal zu übertragen. Allerdings darf man hier nicht vergessen, daß zwischen den Übertragungseigenschaften eines massiven E-Gitarrenkorpus und einem Resonanzkorpus einer Akustikgitarre Welten liegen. Eine Elektrogitarre ist eben darauf optimiert OutE zu maximieren, was automatisch zu einer Verringerung von OutA führt. Der akustische Klang einer massiven Les Paul ist also keinesfalls mit dem einer ordentlichen Westerngitarre zu vergleichen.
Akustische Gitarren mit eingebauten Tonabnehmern oder Mikrofonen sind klanglich auch nicht immer überzeugend, denn um die Anfälligkeit für Rückkopplungen zu senken, wird ein solcher Korpus immer etwas steifer konstruiert. So richtig "voll" und "satt" klingen solche Instrumente dann nicht. Dieses fehlende Etwas läßt sich dann am Verstärker zufügen, sodas insgesamt schon ein gutes Ergebnis entstehen kann.
Ulf
(Die korrigierte und erweiterte Version dieses Artikels findet sich in der Knowledge-Base der Guitar-Letter)

